The same articles about trading strategy over-fitting are repackaged and served to the financial community at regular intervals. Although “over-fitting” is a valid concern, there are some other even more serious issues rarely dealt with in academic papers because they are not easy for earning tenure credits.
Academics have generated so much noise about “over-fitting” to the point that the many in the practitioner community are scared to click on “backtest” button.
Over-fitting is a valid concern. Practitioners have known and understood over-fitting since the 90s when backtesting became popular and called it “over-optimization.”
Over-optimization occurs when the model parameters are fitted on historical data to generate desirable performance. This involves multiple trials referred to as “multiple comparisons” in modern terminology.
There is nothing new here, practitioners have known and understood these problems for many years and academia has contributed next to nothing in dealing with them.
In addition, frequent use of backtesting increases data-mining bias.
Every model when tested is “fitted” on historical data and it is maybe “over-fitted” or “over-optimized” with respect to some arbitrary objective function.
Academics have not provided a sound methodology for distinguishing between “over-fitted” strategies that are going to fail and those that will continue to work well for many years into the future, even decades.
This has probably caused high Type-II error (missed discoveries) to practitioners who follow academic advice for correcting for multiple trials. In essence, some practitioners may have been deprived of potential alpha by claims from people with little or no skin-in-the-game who fight for tenure credits.
I discuss some of these issues in my paper Limitations of Quantitative Claims About Trading Strategy Evaluation.
Expectation convergence is a much more serious issue than over-fitting. This occurs when the average trade of a trading strategy takes long to converge to the mean of the distribution (a.k.a. expectation) due to insufficient sample. This can cause serious underperformance as compared to backtesting result and be a cause of abandoning a strategy.
For example, trend-following strategies tested over many decades will usually generate only a small number of trades in forward samples. The average trade may take long time to converge to the expectation. Below is an example.
A fair coin is tossed with +5 gain for heads and -1 loss for tails. Note that this may be an abstract model of a trend-following strategy with payoff ratio of 5 and 50% win rate. What is a sufficient sample for the average trade to converge to expectation?
The simulation below shows one random path and the convergence to expectation, which is 2 in this case, 0.5 × (5 – 1).
For this random path in time domain, it takes hundreds of trades for the average trade to converge to expectation. The failure after a few dozens of trades may be wrongly attributed to “over-fitting.”
But expectation convergence is slow and probability theory is hard.
What about a trading strategy with high win rate but lower payoff ratio?
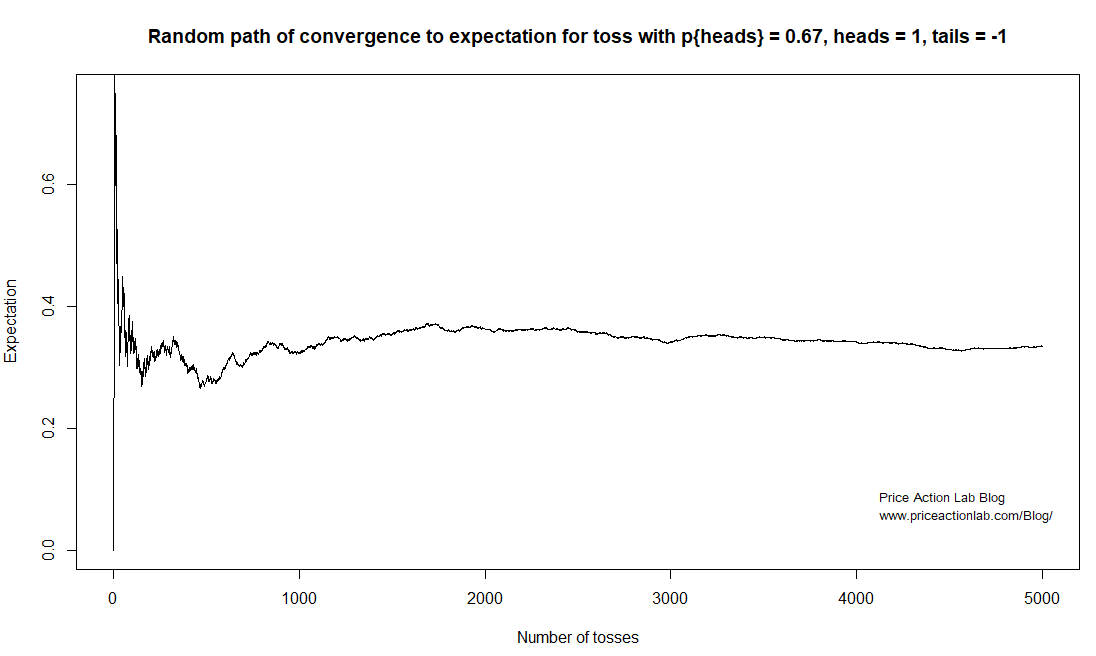
A coin with probability of heads equal to 0.67 is tossed with +1 gain for heads and -1 loss for tails. The simulation below shows one random path and the convergence to expectation, which is 0.34 in this case, 0.67 – 0.33.
For this particular path it took nearly 2000 trades for the average trade to converge to the expectation. For about 500 trades, the average trade fell close to 0.25.
Therefore, “over-fitting” may be an issue but being paranoid about it may even cause Type-II errors. Convergence to expectation is a real problem.
How does one design strategies that converge to expectation in forward samples as fast as possible? I’m not aware of any academic article on this subject. There may be some but I haven’t seen or heard the subject discussed.
In other words, due to slow convergence, some good strategies may never realize their potential in forward application and be abandoned.
Faster trading doesn’t necessarily mean faster convergence because the sufficient sample size may be higher too.
Here are then the three main factors that affect strategy performance and over-fitting is not one of them:
Transaction costs: the higher the sufficient sample required for expectation convergence, the higher the transaction (and slippage) cost will be and convergence may never be reached.
Luck: A time-domain path that will speed expectation convergence. Not all paths are the same and some are better, some are worse and some are even bad.
Regime changes: Failure due to regime changes are not necessarily related to over-fitting. See my paper I quoted above for more details.
Some issues to think about. If you are going to write an academic paper on expectation convergence for trading strategies, a reference to this article will be appreciated.
Disclaimer: No part of the analysis in this blog constitutes a trade recommendation. The past performance of any trading system or methodology is not necessarily indicative of future results. Read the full disclaimer here.
Charting and backtesting program: Amibroker. Data provider: Norgate Data
If you found this article interesting, you may follow this blog via RSS or Email, or in Twitter
Price action Lab premium Content: By subscribing you have immediate access to hundreds of articles. Premium Insights subscribers have immediate access to more than a hundred articles, Premium Articles and Market Signals subscribers have immediate access to hundreds of articles that include the trader education section and All in One subscribers have access to all past premium content. Click here for more details.